SVM

SVM is the initials of Support Vector Machine which is a commonly used machine learning algorithm for binary as well as multi class classification tasks and for regression tasks also.

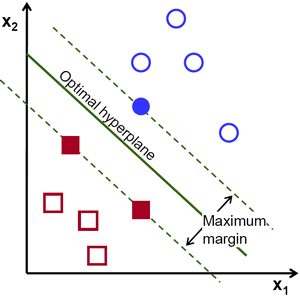
On a surface level SVM is basically an optimization problem involving maximization of the distance between the decision boundary separating the classes. Now the question arises why should we use this instead of a neural network ,this is because SVM searches for the optimal hyperplane as contrary to neural network which returns a hyper plane which could be or couldn’t be optimal depending on the number of iterations and other hyper parameters

So the basic premise of SVM is that it uses a line in case of 2D and hyperplane in case of higher dimension to separate or classify the given data.

There are two types of SVM hard margin and soft margin SVM ,lets first look at the hard margin SVM and then we extend it to soft margin SVM.

Hard margin SVM :

General equation of hyperplane is $(w^T\cdot x+b) = 0$

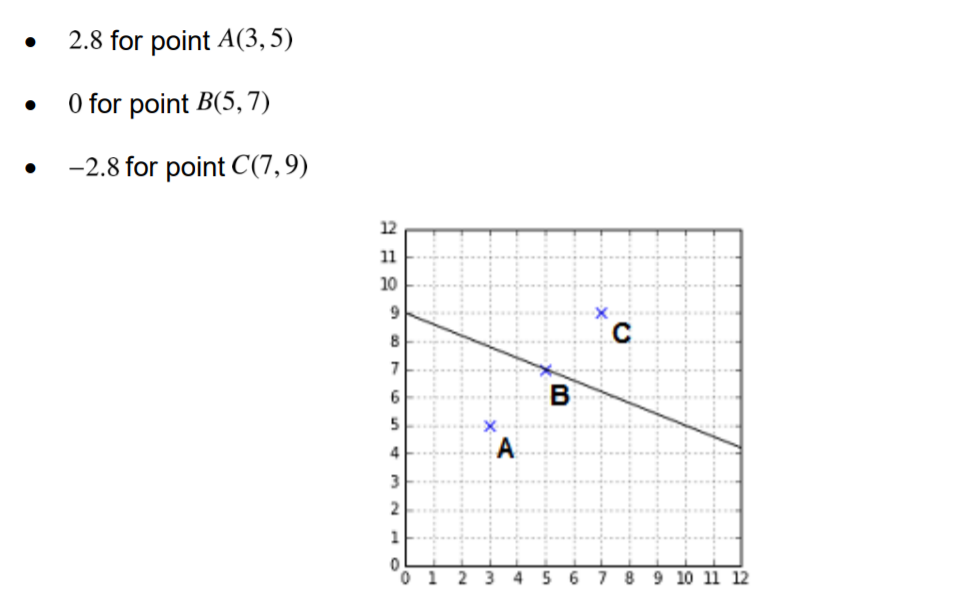
Now first we find out the margin of the hyperplane using the given data. Margin of a hyperplane is the closest distance of a point from the hyperplane in the dataset

Once we have our margin the next task is the find out our $w(weights)$ and $b(bias)$ so that the calculated margin can be maximized. A point to note is that the value of max margin will be same on both side of the hyperplane.

Distance from a point to hyperplane is given as $ \frac{|w^T\cdot x+b|}{||w||}\ $ $where \, \, ||w|| = w^T \cdot w$

Now we calculate distance for each point in the dataset and choose the minimum one.

$M =$ $min(\frac{|w^T\cdot x+b|}{||w||}\ )$

This expression can be reformulated as

$M = $ $(\frac{1}{||w||}\ min(|w^T\cdot x+b| )$

In the above minimization the variable is $x$ and since $w$ is independent of $x$ so we can take it out of the minimization expression. We will use a trick to reduce our minimization problem. We assume that $min(|w^T\cdot x+b|)=1$

Why this assumption holds can be understood by the following example, Let us assume M turns out to be $ \delta $,therefore

$w^T\cdot x+b=\delta$

$(w^T/\delta)\cdot x+b/\delta=1$

Division with $ \delta $ is valid since only the magnitude of $w$ changed and not its direction so this just generates a parallel hyperplane. Also $ \delta $ doesn’t effect out optimization problem as it can be taken out of the expression as it is a constant.

So what this shows is that any margin value can be scaled to 1,hence the assumption can be made that

$min$ $(|w^T\cdot x+b|)=1$

$Therefore \, \, M = $ $\frac{1}{||w||}$

The next step is to maximize the calculated margin so that the classes are as far apart as possible. $max(\frac{1}{||w||})$

This can be restated as $min(||w||)$

Now we have our optimization statement we can focus on the constraints bounding our problem. The basic thing needed to understand the constraints or the limiting conditions is that when we input a point in the equation of hyperplane the sign of the result tells us on which side does the point lie wrt to the line, given that the point is not on the hyperplane.

Example:

This can be formulated as -

$(w^T\cdot x+b) > 0$

$(w^T\cdot x+b) = 0$

$(w^T\cdot x+b) < 0$

Since our class labels$(y)$ are either 1 or -1,we can reformulate above three equations as $y(w^T\cdot x+b) \geq 0$

We have one more constraint as $min(|w^T\cdot x+b|) = 1$

The above two can be expressed as

$y(w^T\cdot x+b) \geq 1 $

The final expression is

$min$ $(||w||) \, \, where \, \,||w|| = w^T \cdot w $

$subject \, \, to\, $ $y(w^T\cdot x+b) \geq1$